Volumen de un trapecio

Volumen de un prisma triangular

Sin embargo, puede ser importante. Ser capaz de calcular el volumen te permitirá, por ejemplo, calcular el espacio de que dispones para hacer una mudanza, el espacio que necesitas en la oficina o la cantidad de mermelada que puedes meter en un tarro.
En el sistema imperial/inglés, las medidas equivalentes son onzas líquidas, pintas, cuartos de galón y galones, que no se traducen fácilmente en pies cúbicos. Por lo tanto, es mejor ceñirse a las unidades de volumen líquido o sólido.
La forma de referirse a las diferentes dimensiones no cambia el cálculo: puedes, por ejemplo, utilizar «profundidad» en lugar de «altura». Lo importante es que las tres dimensiones se multiplican entre sí. Puedes multiplicar en el orden que quieras, ya que no cambiará la respuesta (para más información, consulta nuestra página sobre la multiplicación).
Esta fórmula básica puede ampliarse también para el volumen de cilindros y prismas. En lugar de un extremo rectangular, simplemente tienes otra forma: un círculo para los cilindros, un triángulo, un hexágono o, de hecho, cualquier otro polígono para un prisma.

Volumen del cuadrilátero…

El prisma trapezoidal, tiene 6 caras, 2 de ellas son trapecios y forman las bases en cada extremo del prisma, son caras paralelas, tiene 12 aristas y 8 vértices. Si hacemos un corte transversal en cualquier parte de su longitud, mantiene la figura de un trapecio en las bases.
Podemos encontrar muchos objetos que se asemejan a un prisma trapezoidal, ejemplos de objetos con forma de prisma trapezoidal son: algunos pupitres escolares que tienen forma trapezoidal, pero al tener grosor hay que clasificarlos como prismas trapezoidales. Otro objeto que a veces se considera un prisma trapezoidal son los clásicos lingotes de oro que vemos en las películas de Hollywood, pero en realidad no lo son. Los lingotes de oro tienen los lados inclinados, por lo que la forma se clasifica como una pirámide rectangular truncada.¿Se te ocurren otros ejemplos? deja un comentario en la sección de comentarios al final de la página.
Para calcular el volumen de un prisma trapezoidal puedes utilizar la fórmula del volumen de todo prisma, en la que el área de la base se multiplica por su longitud. En este caso la base del prisma trapezoidal es un trapezoide, por lo que el área del trapezoide que forma la base se multiplica por la longitud. Para obtener el área de un trapezoide hay que sumar la base corta y la base larga del trapezoide y dividir la suma por 2, luego multiplicar por la altura del trapezoide y finalmente multiplicar por la longitud del prisma. También puedes utilizar la calculadora en línea para calcular automáticamente el volumen de la piedra angular.

Hoja de trabajo del volumen de un prisma trapezoidal

Kathryn ha enseñado matemáticas en la escuela secundaria o en la universidad durante más de 10 años. Tiene un doctorado en Matemáticas Aplicadas por la Universidad de Wisconsin-Milwaukee, un máster en Matemáticas por la Universidad Estatal de Florida y una licenciatura en Matemáticas por la Universidad de Wisconsin-Madison.
Los prismas trapezoidales son sólidos tridimensionales. Están formados por dos trapecios congruentes conectados entre sí por cuatro rectángulos. Esta lección incluirá la definición y cómo encontrar el área de la superficie y el volumen de estos sólidos.
Prisma trapezoidal IntroducciónEl término prisma trapezoidal puede no resultarte familiar. Si alguna vez te has fijado en la forma de la mayoría de los ladrillos circulares para hogueras, entonces estarás familiarizado con los prismas trapezoidales. Se parecen a un ladrillo típico, excepto que un lado es más corto que el otro. Esta lección trata sobre la descripción de un trapecio y un prisma trapezoidal. También se tratarán las fórmulas para el área de la superficie y el volumen de estos prismas.
Cómo hallar el volumenPara hallar el volumen, la cantidad de espacio en el interior de un sólido, necesitarás hallar el área de la base del trapecio y luego multiplicarla por la altura del prisma. Ten en cuenta que hay dos alturas diferentes. Está la altura del trapecio, que utilizarás para hallar el área del trapecio. También está la altura del prisma, que necesitarás para hallar el volumen del prisma trapezoidal. La fórmula del volumen del prisma trapezoidal es volumen=Hh(b1+b2)/2. En esta fórmula, b1 y b2 son la base del trapecio. La minúscula h es la altura del trapecio, y la mayúscula H es la altura del prisma. EjemplosEste es nuestro primer ejemplo: Encuentra el área de la superficie de un prisma trapezoidal que tiene bases de 3 y 5 pies, lados de 3 pies, una altura del trapezoide de 2.83 pies y una altura del prisma de 5 pies.

El volumen de la paralogr…

La mayoría de los problemas relativos a los prismas trapezoidales se refieren a formas simétricas, es decir, la altura en todos los lados es constante. Pero, en ciertas estructuras prismáticas, la altura puede diferir en diferentes aristas dando lugar a un prisma trapezoidal asimétrico.
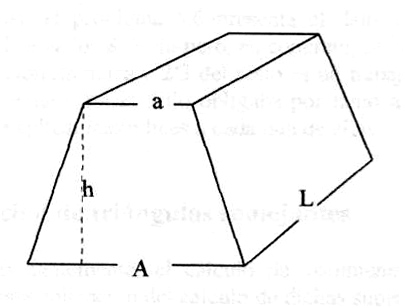
Un prisma trapezoidal es una forma geométrica tridimensional que consta de una forma trapezoidal o de trapecio en una sección transversal, y de un rectángulo en las otras secciones transversales. Los componentes más importantes de esta forma geométrica son su longitud, altura, altura oblicua, anchura de la base y anchura superior. Conociendo sus valores, es posible calcular el volumen y la superficie de un prisma trapezoidal.
A continuación se explica paso a paso cómo calcular el volumen de un prisma trapezoidal y su fórmula. En la mayoría de los casos, los cálculos se pueden realizar si sólo se conocen la anchura, la altura y la longitud de la parte inferior y superior. Pero cuando se conoce la altura oblicua en lugar de la altura real, entonces hay que utilizar una fórmula diferente.
Con el diagrama anterior se entienden todos los componentes de un prisma trapezoidal. Digamos que se conocen los valores del ancho superior e inferior, la longitud y la altura de la figura. Entonces la fórmula para calcular su volumen es: